 |
NMSIS-DSP
Version 1.4.1
NMSIS DSP Software Library
|
 |
NMSIS-DSP
Version 1.4.1
NMSIS DSP Software Library
|
a[n] and b[n], with lengths n1 and n2 respectively, are zero padded so that their lengths become N, which is greater than or equal to (n1+n2-1) and is a power of 4 as FFT implementation is radix-4. The convolution of a[n] and b[n] is obtained by taking the FFT of the input signals, multiplying the Fourier transforms of the two signals, and taking the inverse FFT of the multiplied result. A[k] = FFT(a[n],N) B[k] = FFT(b[n],N) conv(a[n], b[n]) = IFFT(A[k] * B[k], N)where
A[k] and B[k] are the N-point FFTs of the signals a[n] and b[n] respectively. The length of the convolved signal is (n1+n2-1).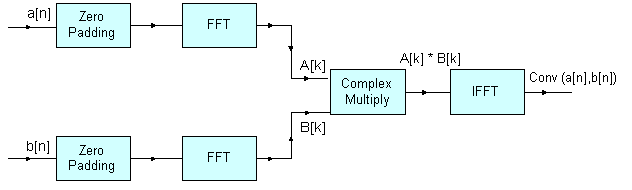
testInputA_f32 points to the first input sequence srcALen length of the first input sequence testInputB_f32 points to the second input sequence srcBLen length of the second input sequence outLen length of convolution output sequence, (srcALen + srcBLen - 1) AxB points to the output array where the product of individual FFTs of inputs is stored.